2.3.4 Simulation of Reliability Policies

To confirm the efficiency of the adaptive parity caching, we simulated the parity reliability policies on our trace-driven simulator , using the HP disk I/O traces  .

For the simulation we used 12 days of disk I/O traces of the most frequently accessed disk in the traces, and simulated 8 storage servers and one parity server, connected by an ATM network. We have simulated four policies :

• An Unreliable policy, which uses a block cache to reduce the device latency. This policy has the optimum performance.
• The Parity Caching policy as described in section 2.3.2.
• The Adaptive Parity Caching policy, defined in section 2.3.3, using two stream caches (P = 2).
• The Mirroring policy described in section 2.3.1. Mirroring requires 100% extra space.

The disk block size was 1024 bytes, and the parity caches stored 8 disk blocks for each server. The cleaning method we used, cleaned the most redundant parity groups first, by reading the full blocks and writing new non-redundant parity groups. The redundant parity groups were cleared. In the parity policies redundancy cleaning was performed only when the disk was full and empty space was needed.

The results of our simulations are presented in figures 6 and 7, and in the table 1. Figure 6 shows the execution time curve for each policy, including cleaning time for the parity caching policies. The basic conclusion derived from this figure is that the execution time for adaptive parity caching is only 11% worse of the optimum unreliable execution time, even when only 20% extra space is given.

Figure 7, which draws the curves of the cleaning time for the parity caching policies, shows clearly that the adaptive caching policy needs much less cleaning time than simple parity caching. For example, cleaning time for the adaptive parity caching is 30% lower than the cleaning time for simple parity caching, when we give 20% extra space. This also means that the adaptive parity caching policy generates less redundant parity blocks.

 
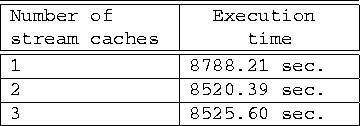
Table 1:   Cleaning time using a variable number of stream caches for 20% extra storage space.

Table 1 shows execution times for a variable number of stream caches for 20% extra space. The adaptive parity caching policy with one stream cache is equivalent to the (non-adaptive) parity caching policy. It is very interesting to notice that although there is a significant improvement from one to two stream caches, using more than two stream caches, practically does not affect performance.

 

 

Figure 6: Simulated execution (network) time for three reliability policies. For the trace-driven simulation, we used 12 days of disk traces, and simulated 8 storage servers and one parity server for each parity policy. The time on the Y-axis is the network transfer time in seconds (on an ATM network) needed for executing all the traces.

 

 

Figure 7: Simulated Cleaning cost of Reliability Policies. For the trace-driven simulation, we used 12 days of disk traces, and simulated 8 storage servers and one parity server for each parity policy. The cleaning time on the Y-axis is the network transfer time in seconds (on an ATM network) needed for cleaning the device (each time it was needed to write new blocks).